1995 - 棋盘方格
题目描述
设有一个 N \times M 方格的棋盘 (1≤N≤100,1≤M≤100)
求出该棋盘中包含有多少个正方形、多少个长方形(不包括正方形)。
例如:当 N=2, M=3 时:
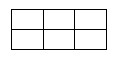
正方形的个数有 8 个:即边长为 1 的正方形有 6 个;边长为 2 的正方形有 2 个。
长方形的个数有 10 个:
即
- 2 \times 1 的长方形有 4 个:

- 1 \times 2 的长方形有 3 个:
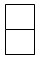
- 3 \times 1 的长方形有 2 个:

- 3 \times 2 的长方形有 1 个:
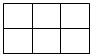
输入
每个测试文件只包含一组测试数据,每组输入两个正整数 n 和 m。
输出
对于每组输入数据,出该棋盘中包含的正方形个数和长方形个数。
样例
输入
2 3
输出
8 10
说明
【来源】1997年NOIP全国联赛普及组
来源
noip复赛
标签