金银岛上有一个迷宫，迷宫由 N 间密室组成，密室的编号为 1 \sim N。每间密室都有且只有唯一的一条单向通道通往下一间密室。部分密室沿着这条唯一的单向通道会走回原密室。每间密室都有一定数量的金币。

请编程计算出，如果单独从每一间密室出发，可以沿着密室之间的单向通道任意的走（可以重复的走已经走过的通道或者密室，同一间密室中的金币只能被统计一次），最多能收集到多少个金币？

第 1 行读入一个正整数 N。

第 2 行有 N 个整数 C_1,\dots,C_N，第 i 个整数 C_i 表示编号为 i 的密室内能搜集到的金币的数量。

第 3 行有 N 个整数 T_1,\dots,T_N，第 i 个整数 T_i 表示编号为 i 的密室通往密室的编号。

输出 N 行，第 i 行输出，如果从编号为 i 的密室出发，最多能收集到的金币的数量。

样例 1 解释

样例 1 的输入数据构成如下所示的图。

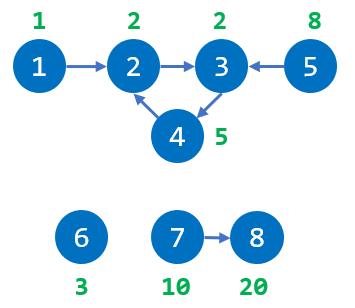
从点 1 出发，可以经过点 1,2,3,4，得到金币和=1+2+2+5=10。

从点 2,3,4 出发，可以经过点 2,3,4，得到金币和=2+2+5=9。

从点 5 出发，可以经过点 5,3,4,2，得到金币和=8+2+5+2=17。

从点 6 出发，可以经过点 6，得到金币和=3。

从点 7 出发，可以经过点 7,8，得到金币和=10+20=30。

从点 8 出发，可以经过点 8，得到金币和=20。

数据范围

对于 20\% 的数据，N \le 10。

对于 40\% 的数据，N \le 1000。

对于 100\% 的数据，1 \le N \le 2 \times 10^5，1 \le C_i \le 10^4。

月赛Tarjan