在一次神秘的数学探险中，你发现了一种神奇的数字表示方法——负二进制。这种方法和我们平常使用的二进制不同，它使用的基数是-2。

在这种方法中，每个数位上只能是0或1，而没有其他数字。

例如，10 的负二进制表示是 110 ，而 -10 的负二进制表示是 1010。

现在，给定一个整数 N，求它在负二进制下的表示。负二进制表示是指，将整数N表示为一个由 0 和 1 组成的字符串 S，使得 S 满足以下条件：

1、S 的第一个字符为 1，或者 S 为 0。

2、 S 表示形式如下：

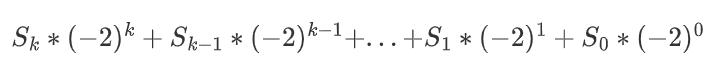
3、{S_0、S_1、...、S_k} 都是 0 或 1。

S 所代表的数值等于 N 。

输入 N

输出 N 的 -2 进制转换的结果

【数据范围】

{−10^9 \le N \le 10^9}

进制转换