聪聪用钢丝网建造了一批同样大小的正方体网箱，将它们拼成了 M \times N 的矩形网格（每个格子都是一个网箱），放在池塘里，专门用来养殖一种凶猛的斗鱼。斗鱼天生好斗，只要旁边有其它斗鱼靠近，哪怕隔着钢丝网，它们都能斗个你死我活，所以每个网箱里最多只能饲养一条斗鱼；而且，两条斗鱼必须在不相邻的网箱（竖直或水平方向）。

另外，聪聪在某些网箱里还安装了养殖设备，这些网箱里也不能养斗鱼。

聪聪想知道，这组网箱一共有多少种可行的饲养方案（至少养一条斗鱼）。由于方案数量比较大，所以只需要求出方案数量对 100000007 的取模结果。

例如：M = 2，N = 2，矩形网格的格局如图所示（蓝色为水，灰色为设备）：

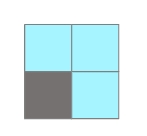
饲养 1 条鱼的方案有 3 种（ 3 个蓝色网箱都可以养鱼）；

饲养 2 条鱼的方案有 1 种（用左上角和右下角的蓝色网箱养鱼）；

这个 2 \times 2 的矩形网格有 4 种饲养方案，4 对 100000007 取模的结果是 4，故输出 4。

第一行输入两个正整数 M 和 N（2 \le M \le 100，2 \le N \le 10），分别表示矩形网格的行数和列数，两个正整数之间以一个空格隔开。

第二行开始输入 M 行，每行 N 个整数（只能是 1 或 0 ），1 表示水，0 表示设备，整数之间以一个空格隔开。

输出一个整数，表示至少养 1 条斗鱼的饲养方案数量对 100000007 取模的结果。

蓝桥杯十五届STEMA考试 C++试卷（23年8月）

蓝桥杯STEMA压状DP